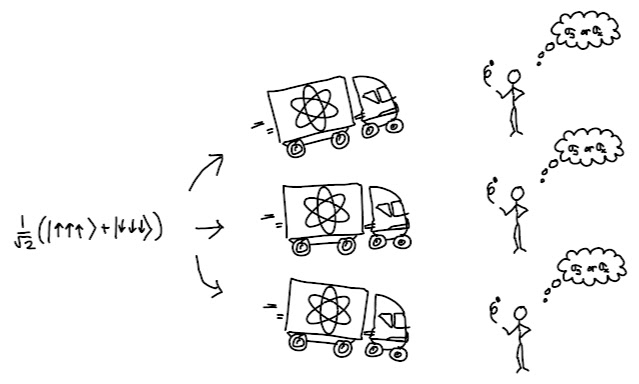
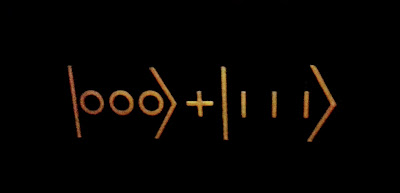Does time exist?

This is perhaps the greatest epiphany of my life. The moment I realized how to neatly summarize my understanding of the science I was learning: Time does not exist. Of course, this is just an interpretation, and a personal one. It may not be true but in it's defence I assert it is consistent with many physicists' view of the world (though they may put it a different way). It may not even make sense to ask whether it is true or not: what does it mean to say that a thing we don't understand, and haven't clearly defined, doesn't exist. But like a lot of ways of thinking about reality, the real question is: Is this helpful? The things we know exist in the world can be divided into two categories: those for which we have direct evidence, and those for which we have indirect evidence. In the former category we have light, sound, touch, smell; in the latter planets, atoms, and waves. Time also belongs to the latter category. We think about the future w...