Three ways to look at the Bell/GHZ experiment

In 1964 John Stewart Bell proposed an experiment to determine whether the results of quantum measurements were truly random, or governed by hidden variables, i.e. state that exists prior to the measurement, but which we don’t have access to. The experiment involved creating a large number of EPR pairs, and firing them at two observers, Alice and Bob, who measure their photon’s polarisation, choosing the $\updownarrow$ direction or the $\nearrow\llap\swarrow$ direction at random. Determining the result of the experiment involves doing a complex statistical calculation to see if something called Bell’s inequality is satisfied or violated. The Bell experiment was first performed by in 1982 by Alain Aspect, and the result, as most commonly interpreted, is that hidden variables can only exist if Quantum Mechanics is non-local, i.e. if it supports faster-than-light causality!

Some time after Bell proposed his experiment, Greenberger, Horne, and Zeilinger suggested an alternative one to answer the same question. Theirs involved three entangled particles instead of two, but did away with the need for any complicated statistics. We shall consider three ways to look at this experiment. All three approaches lead to the same predictions, but they provide different insights into what is going on.

Contents

• Version 1: Three spins
• The mathematics
• Version 2: The quantum computer
• The mathematics
• Version 3: Treating Alice, Bob, and Charlie as quantum mechanical systems
• The mathematics

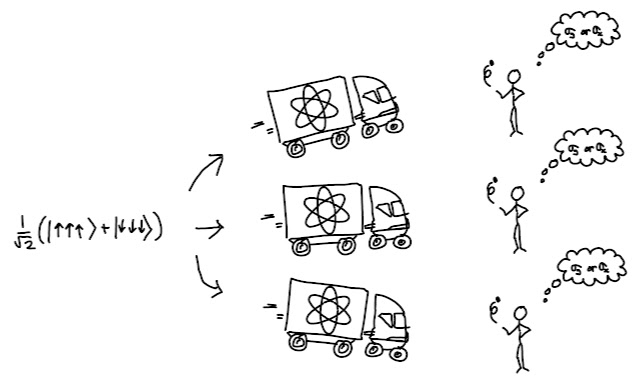
Version 1: Three spins

This version is easy to analyse but provides few hints as to why the results are seen, or how to find a way out of the non-locality paradox.

In this version three spins are entangled in the state $(\lvert \uparrow\uparrow\uparrow \rangle + \lvert \downarrow\downarrow\downarrow \rangle)/\sqrt 2$ and are sent, respectively, to Alice, Bob, and Charlie who are in different locations. After receipt of their spin, Alice, Bob, and Charlie each toss a coin and measure their spin along the X-axis if they get tails, and the Y-axis if they get heads. Critically, all three do this simultaneously so that no information about the coin toss or the measurement result can reach the others before they choose an axis or make a measurement.

The results are that Alice, Bob, and Charlie observe a 50% chance of getting a +1 and a 50% chance of a -1, and this is independent of whether they got H or T in the coin toss. However, when all three get tails (TTT) multiplying together the measurements always results in +1, and when just one gets tails (THH, HTH, or HHT) multiplying them always results in -1. So, for example (TTT, -1, -1, 1) is possible, but (TTT, -1, -1, -1) is not. This result seems to either rule out hidden variables or allow for non-local causality. But why?

Alice knows she gets +1 and -1 each half the time. As far as she is concerned there are two possibilities: 1) the result is determined by hidden variables before she makes her measurement; 2) the result is chosen at random at the exact moment the measurement is made.  She can rule out (1) by a simple thought experiment.  If it were the case then she could label the results she would get if she were to measure along the X-axis $X_1$, and the result she would get if she were to measure only the Y-axis as Y1. Likewise Bob could label his possible results as $X_2$, and $Y_2$, and Charlie could label his $X_3$, $Y_3$.  Alice knows from past experience that $X_1Y_2Y_3$, $Y_1X_2Y_3$ , and $Y_1Y_2X_3$ are always ‑1.  But this would imply that $X_1X_2X_3$ is also always -1 as it is what you get if you multiply the former 3 terms together.  Since $X_1X_2X_3$ is in fact always +1 Alice can rule out (1).  But if her result is chosen only at the moment she makes the measurement then there must be some faster-than-light communication to Bob and Charlie.  For example, if they all decide to measure X and Alice measures a -1, then Bob and Charlie's spins need to get updated instantaneously so that they cannot both measure the same value, and if she measures +1 then Bob and Charlie's spins need to get updated instantaneously so that they must measure the same value.

The mathematics

Let’s see if we can work out why this is the result predicted.

A short reprise on quantum measurement: A measurement in quantum mechanics corresponds to a Hermitian operator.  These always have a set of orthonormal eigenvectors, and so any state can be decomposed as a sum of these.  For example, $\sigma_z$ is the operator corresponding to measurement of a spin along the Z-axis.  It's eigenvectors are $\lvert\uparrow\rangle$ and $\lvert\downarrow\rangle$.  If $\lvert\Psi\rangle$ is a spin pointing along the X-axis then $\lvert\Psi\rangle = \left(\lvert\uparrow\rangle + \lvert\downarrow\rangle\right)/\sqrt 2$. According to the Born rule, eigenvalues are the possible measurement results, and the probability of each result is given by the square of the magnitude of the corresponding eigenvector's coefficient.  So in this example if we were to measure $\sigma_z$ when the state is $\lvert\Psi\rangle$ we'd have a 50% chance of getting +1 and a 50% chance of getting -1.  A consequence of this rule is that if the original state is an eigenvector of the measurement if, and only if, the result is 100% known in advance.

In the case where we have 3 entangled spins the space is a product space $V\otimes V\otimes V$, where $V$ is the space for a single spin, and the measurement that Alice, Bob, and Charlie would make if they got HTH would be the product operator $\sigma_y\otimes\sigma_x\otimes\sigma_y$.  Now, $\sigma_x$ takes $\lvert\uparrow\rangle$ to $\lvert\downarrow\rangle$ and vice versa, whereas $\sigma_y$ takes $\lvert\uparrow\rangle$ to $i\lvert\downarrow\rangle$ and $\lvert\downarrow\rangle$ to $-i\lvert\uparrow\rangle$.  This means that $\sigma_y\otimes\sigma_x\otimes\sigma_y$ takes $\left(\lvert\uparrow\uparrow\uparrow\rangle+\lvert\downarrow\downarrow\downarrow\rangle\right)/\sqrt 2$ to

$$
\begin{align*}
&\frac{1}{\sqrt 2}(
\sigma_y\lvert\uparrow\rangle\otimes
\sigma_x\lvert\uparrow\rangle\otimes
\sigma_y\lvert\uparrow\rangle +
\sigma_y\lvert\downarrow\rangle\otimes
\sigma_x\lvert\downarrow\rangle\otimes
\sigma_y\lvert\downarrow\rangle) = \\
&\frac{1}{\sqrt 2}(
i^2
\lvert\downarrow\rangle\otimes
\lvert\downarrow\rangle\otimes
\lvert\downarrow\rangle +
(-i)^2
\lvert\uparrow\rangle\otimes
\lvert\uparrow\rangle\otimes
\lvert\uparrow\rangle) = \\
-&\frac{1}{\sqrt 2}(\lvert\uparrow\uparrow\uparrow\rangle +
\lvert\downarrow\downarrow\downarrow\rangle)
\end{align*}
$$

This tells us that $(\lvert\uparrow\uparrow\uparrow\rangle + \lvert\downarrow\downarrow\downarrow\rangle)/\sqrt 2$ is an eigenvector of $\sigma_y\otimes\sigma_x\otimes\sigma_y$ with eigenvalue -1, i.e. that when the coins come up HTH, the product of the measurements is 100% guaranteed to be -1, and likewise for THH, and HHT.

A similar calculation shows that $(\lvert\uparrow\uparrow\uparrow\rangle + \lvert\downarrow\downarrow\downarrow\rangle)/\sqrt 2$ is also an eigenvector of $\sigma_x\otimes\sigma_x\otimes\sigma_x$, but this time with eigenvalue 1.  This tells us that when Alice, Bob, and Charlie throw TTT the product of their measurements is 100% guaranteed to be +1.

Version 2: The quantum computer

This version is a bit more confusing but more clearly illustrates how destructive interference causes some results to be eliminated from the set of possible outcomes.

In this version we use a quantum computer. Instead of spins $\lvert \uparrow \rangle$ and $\lvert \downarrow \rangle$ we talk about qbits $\lvert 0 \rangle$ and $\lvert 1 \rangle$, and instead of products of +1s and -1s we talk about the parities of 3-tuples such as 011.

In the diagram above, each horizontal line represents one qbit, and each rectangle is a "gate".  Unlike measurements, which "collapse" the wavefunction, gates represent a change-over-time of the wavefunction.  Measurement is non-reversible since, for example, a measurement of a single qbit system leaves it in just one of two states, whereas the original state space is infinite.  By contrast, a gate is completely reversible, in the same way that the Schrödinger equation is symmetric in forward and reverse time.

The mathematics

Gates are represented by the following unitary operators:

• The first gate applies to just Alice's qbit and is called a Hadamard gate.  It takes
• $\lvert 0\rangle$ to $(\lvert 0\rangle + \lvert 1\rangle)/\sqrt 2$, and
• $\lvert 1\rangle$ to $(\lvert 0\rangle - \lvert 1\rangle)/\sqrt 2$
• The second and third gates are CNOT, or Controlled NOT, operators.  These apply to the product space of two qbits.  CNOT takes
• $\lvert 0x\rangle$ to $\lvert 0x\rangle$, and
• $\lvert 1x\rangle$ to $\lvert 1\bar{x}\rangle$.
• The $R_x(\pi/2)$ gates rotate a single qbit about the X-axis in the Bloch sphere.  The exponents$h_A$, $h_B$, and $h_C$ indicate that Alice, Bob, and Charlie should only implement this gate if they toss heads.  This gate takes
• $\lvert 0 \rangle$ to $(\lvert 0\rangle -i \lvert 1\rangle)/\sqrt 2$, and
• $\lvert 1\rangle$ to $(-i\lvert 0\rangle + \lvert 1\rangle)/\sqrt 2$.
• The $R_y(-\pi/2)$ gates rotate a single qbit about the Y-axis in the Bloch sphere.  The exponents $t_A$, $t_B$, and $t_C$ indicate that Alice, Bob, and Charlie should only implement this gate if they toss tails.  This gate takes
• $\lvert 0 \rangle$ to $(\lvert 0\rangle - \lvert 1\rangle)/\sqrt 2$, and
• $\lvert 1\rangle$ to $(\lvert 0\rangle + \lvert 1\rangle)/\sqrt 2$.
• The final rectangles represent measurement along the Z-axis, which is defined by the eigenvectors $\lvert 0\rangle$ and $\lvert 1\rangle$.

With this background we can calculate each of the states $\lvert\Psi_1\rangle$, $\lvert\Psi_2\rangle$, $\lvert\Psi_3\rangle$, $\lvert\Psi_4\rangle_{hht}$, and $\lvert\Psi_5\rangle_{hht}$ (the hht subscript indicates that this is the situation in which the coin tosses obtained the result HHT).

$$
\require{cancel}
\begin{align*}
\lvert \Psi_1 \rangle &= \lvert 000\rangle \\
\\
\lvert \Psi_2 \rangle &= \frac{1}{\sqrt 2}(\lvert 000\rangle +
\lvert 100\rangle) \\
\\
\lvert \Psi_3 \rangle &= \frac{1}{\sqrt 2}(\lvert 000\rangle +
\lvert 111\rangle) \\
\\
\lvert \Psi_4 \rangle_{hht} &=  \frac{1}{2\sqrt 2}(\\
&\lvert 000\rangle -i\lvert 010\rangle -i \lvert 100\rangle -
\lvert 110 \rangle \\
 -&\lvert 001\rangle -i\lvert 011\rangle -i \lvert 101\rangle +
\lvert 111 \rangle) \\
\\
\lvert \Psi_5 \rangle_{hht}&= \frac{1}{4}(\\
   &\cancel{\lvert 000\rangle} -\lvert 001\rangle - i\lvert
010\rangle +i\cancel{\lvert 011 \rangle} \\
 -i&\lvert 100\rangle +i\cancel{\lvert 101\rangle} -
\cancel{\lvert 110\rangle} +\lvert 111 \rangle \\
 -&\cancel{\lvert 000\rangle} -\lvert 001\rangle -i\lvert
010\rangle -i\cancel{\lvert 011 \rangle} \\
 -i&\lvert 100\rangle -i\cancel{\lvert 101\rangle}
+\cancel{\lvert 110\rangle} +\lvert 111 \rangle
)
\end{align*}
$$

This shows that only parity 1 combinations remain.  A similar calculation for $\lvert \Psi_5 \rangle_{ttt}$ leaves only parity 0 combinations! This shows how the possible outcomes can be described to be as a result of interference.

Version 3: Treating Alice, Bob, and Charlie as quantum mechanical systems

Is there any reason we cannot treat everything in the experiment, including Alice, Bob, and Charlie, as quantum mechanical? We know the participants are perfectly isolated from each other by distance and the speed of light, so there’s really no problem in this. In this treatment the initial state can be represented as a superposition in which each term represents a pre-determined outcome. The only problem is that you have to believe in the multiverse.

The qbits Alice, Bob, and Charlie start off $\lvert h \rangle$, for heads, giving an initial state for the entire system of $\lvert \Psi_1 \rangle =\lvert hhh 000 \rangle$. To get to $\lvert \Psi_2 \rangle$ the lower subsystem is entangled in the 3-qbit Bell state $(\lvert 000 \rangle + \lvert 111 \rangle)/\sqrt 2$ as before, but in addition to this each of Alice, Bob, and Charlie are transformed by Hadamard gates. This leaves the entire system in the product state

$$
\lvert \Psi_2\rangle = \frac{1}{4}\sum_{a,b,c
\in \{h,t\}}{\lvert abc \rangle} \otimes (\lvert 000 \rangle +
\lvert 111 \rangle)
$$

The $R_x(\pi/2)$ rotation gates are now controlled gates that only occur if the corresponding participant state is $\lvert h \rangle$. The $X$ gate swaps $\lvert h \rangle$ and $\lvert t \rangle$, so the $R_y(-\pi/2)$ are also controlled but only occur if the participant state is $\lvert t \rangle$. In this version $\lvert \Psi_3 \rangle$ is a complicated state like

$$
\lvert \Psi_3\rangle = \sum_{a,b,c \in
\{h,t\}}\sum_{x,y,z \in \{0,1\}} \psi_{abcxyz}\lvert abcxyz
\rangle
$$

in which certain coefficients, such as $\psi_{ttt111}$ or $\psi_{hht110}$ have value 0. This is the multiverse interpretation in which collapse never occurs!

The mathematics

The above picture shows no interaction with any classical system and so we are allowed to treat all the gates as a single unitary operator $U$. If we were to append a measurement in the computational basis, its operator would be $Z^{\otimes 6}$ where $Z$ is the pauli Z matrix. We could then treat the entire circuit as a single measurement. What operator $A$ would that correspond to?

We know that if we were to start off with state $\lvert \Psi_1 \rangle = U^\dagger \lvert hhh000 \rangle$ the final result would be 100% guaranteed to be $\lvert hhh000 \rangle$. A similar thing would be the case for all the other combinations of 3 h’s and t’s, and 3 0’s and 1’s. The only initial states which have known final states following a measurement are its eigenvectors. This means we know the eigenvectors of $A$ must be

$$
U^\dagger \lvert abcxyz \rangle \ \dots a,b,c \in \{h,t\}, x,y,z \in \{0,1\}
$$

Knowing the eigenvectors and eigenvalues uniquely identifies the operator, so we must have that

$$
A = U^\dagger Z ^{\otimes 6} U
$$

In the illustration above we did not start off in an eigenstate of $A$, but instead the state

$$
\lvert \Psi_1 \rangle = \lvert hhh000
\rangle .
$$

If we were to decompose this using the orthonormal set of eigenvectors $U^\dagger \lvert abcxyz \rangle $ we would find that all the terms where there’s one t and two h’s in $abc$, and $xyz$ has parity zero, are missing. Likewise all the terms where there are three t’s in $abc$, and $xyz$ has parity one, are missing.

Viewed this way there is no need to explain the outcomes of any collapse as no collapse occurs. Subjectively when Alice, Bob, and Charlie come together to compare results, all that happens is that they determine which term in the original superposition they were in all along.