Regular solid clock

A while ago I was pondering the symmetries of Platonic solids and a strange thing occurred to me.  The number of rotational symmetries for the tetrahedron, cube, octahedron, dodecahedron, and icosahedron are 12, 24, 24, 60, and 60 respectively $^\dagger$.  These happen to match the number of hours in an afternoon (I'm told mornings have the same number), the number of hours in a day, the number of minutes in an hour,  and the number of seconds in a minute. This is probably a coincidence due to the fact that the Babylonians (who created our time system) used base 60, and 60 is divisible by a lot of small numbers.  But it's nice to imagine, and just possible, that they were thinking about regular solids when then came up with the system for measuring time. 

It's just turned midnight

When this occurred to me a picture jumped into my head, which I've tried to recreate above.  It's a clock built from platonic solids.  Every second one or more of them rotates and the numbers at the top of the front face give you the time.  In the picture I've used dodecahedrons for minutes and seconds but either or both could be replaced by icosahedrons. The hour digit is represented by a cube which has 24 symmetries, so this is a 24 hour clock.  But this digit could be replaced by an octahedron, or a tetrahedron if we want a 12 hour clock. 

There was just one problem with this idea: I couldn't work out how to find a single rotation which could be repeated over and over to cycle through the hours 00,..., 23 (or the minutes 00,...,59 or the seconds 00,...,59).  So I parked the idea.  However, as I described in a recent post, I have now figured out how to represent the rotational symmetries of a regular solid, and build a Cayley graph for the group.  The representation is $\langle a,b \vert a^n=b^m=(ab)^2=1\rangle$ where $a$ is a clockwise rotation of one face and $b$ is a clockwise rotation around one of that face's vertices.

Since this is a different group to $\langle a \vert a^{24}=1\rangle$ it is clear that we cannot find a single rotation that can be repeated to cycle through all the values printed on the solid. However, it is possible that a pattern of $a$s and $b$s plus their inverses might exist that does the job.  Finding this is equivalent to finding a Hamiltonian cycle around the Cayley graph, interpreted as an undirected graph.  A Hamiltonian cycle is a closed path around the graph that visits every node just once.

I've applied brute force to find a Hamiltonian cycle in the Cayley graph for the rotational symmetries of the cube, and the result is shown below.  Remember that the Cayley graph for $\langle a,b \vert a^n=b^m=(ab)^2=1\rangle$ is just the original Platonic solid with the edges replaced by rectangles and the vertices replaced by $m$-gons.

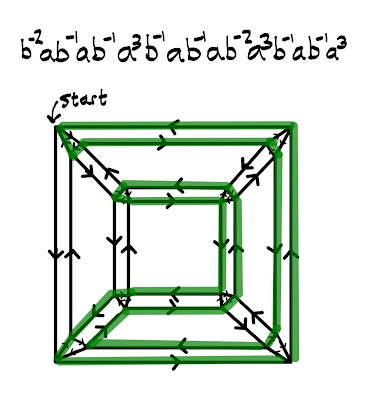24 applications of $a$, $b$, or $b^{-1}$ that visits each rotational symmetry once and returns the cube to its starting position

It turns out you can find such a cycle in every regular solid's Cayley graph (I know this because I tried)$^{\dagger_2}$.

So there you have it, a clock made from 3 regular solids.  Every tick one or more of the solids (representing hours, minutes, and seconds) rotates.  Each rotation is either single rotation of the front face (specifically $a$ or $a^{-1}$) or a single rotation about one of that face's vertices (specifically $b$ or $b^{-1}$). It comes in 12 and 24 hour variants, and every one of the 5 Platonic solids can be used if desired. Nice. 


FOOTNOTES 

  • $\dagger$ The reason 24 and 60 are both duplicated in this list is that the cube and the octahedron are duals, as are the dodecahedron and the icosahedron. The rotational symmetry group of a solid and its dual are isomorphic with the isomorphism taking a rotation of a face to a rotation about a vertex and v.v.
  • $\dagger_2$ I was hoping to find a simple algorithm to generate the cycle but that seems a bit unlikely given that, according to Wikipedia, the task of finding a Hamiltonian path or cycle in a graph is an NP complete problem.  The same article also pointed out that it has been proved that any 4-connected graph (a graph in which removing up to 3 nodes cannot break it into multiple pieces) must have a Hamiltonian cycle.  It's easy to see that all the Cayley graphs are indeed 4-connected and so this does at least give some reason why Hamiltonian cycles should exist in all of them.

Comments

Post a Comment

Popular posts from this blog

How To Make ASCII Diagrams Beautifuller

Image
I've discovered an excellent tool in asciiflow.com .  The website makes it really easy to create ASCII box diagrams like this They put these things in fruit machines you know! This is ideal for source code banners, which I think should contain helpful documentation - but most programmers think it's a good place for the COPYRIGHT information and nothing else. But wait! we can make it beautifuller... and easier to read... by replacing some of the ASCII characters with ones available in UTF-8: There!  Isn't that better?  (Although some purists may object to non-ASCII characters in your code base.) SOURCE CODE: #!/usr/bin/python2 # coding: utf-8 # + gets converted in different ways depending on it's 4 neighbours # # . N . { nsew(N,S,E,W) has bit 3 set if N in "+|<>" # W + E { nsew(N,S,E,W) has bit 2 set if S in "+|<>" # . S . { nsew(N,S,E,W) has bit 1 set if W in "+-^v" # { nsew(N,S,E,W) has bit 0 set if E ...
Read more

Why growth is falling in all developed countries (as a long term trend)

Image
In this post I argue that economic growth is not the normal state of affairs, it is a blip caused by the discovery of a one-off resource of non-renewable energy.   The logistic equation $$ \frac{dy}{dt} = y(1-y) $$ Here's a simple model.  Humans discover an exploitable but limited resource and start consuming it.  The amount consumed, $y(t)$, is a function of time.  The general form of the equation is $\frac{dy}{dt} = \alpha y (\beta - y)$, but if you choose the right units $\alpha$ and $\beta$ both become $1$. Why should this work, in principle? Early on, the factor $1-y$ is approximately $1$ and can be ignored.  So the model states that annual consumption $dy/dt$ starts off proportional to $y$.  In other words, $y$ grows exponentially at first.  This could happen if exploiting the resource enables further exploitation of the resource.  For example, suppose a few humans are shipwrecked on an island with 1000 trees: they take ages to cut down the ...
Read more

Three ways to look at the Bell/GHZ experiment

Image
In 1964 John Stewart Bell proposed an experiment to determine whether the results of quantum measurements were truly random, or governed by hidden variables, i.e. state that exists prior to the measurement, but which we don’t have access to. The experiment involved creating a large number of EPR pairs, and firing them at two observers, Alice and Bob, who measure their photon’s polarisation, choosing the $\updownarrow$ direction or the $\nearrow\llap\swarrow$ direction at random. Determining the result of the experiment involves doing a complex statistical calculation to see if something called Bell’s inequality is satisfied or violated. The Bell experiment was first performed by in 1982 by Alain Aspect, and the result, as most commonly interpreted, is that hidden variables can only exist if Quantum Mechanics is non-local, i.e. if it supports faster-than-light causality! Some time after Bell proposed his experiment, Greenberger, Horne, and Zeilinger suggested an alternativ...
Read more