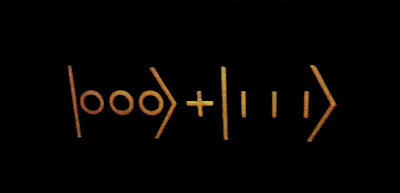Dork Scratchings

Hobbit hole, Chalkney Woods (Homunculum cuniculum) Stinkhorn, Sandringham (Phallus Impudicus) Wild dog with pliosauroid fossil, Sandringham (Canis Poodiculous)

I'm old enough to remember when holograms first appeared commercially.  I remember being amazed and trying to look behind to see if it wasn't just a 3-dimensional object masquerading as a 2-dimensional object (masquerading as a 3-dimensional object).  It must have looked like when you show a chimp a mirror and it tries to reach behind it to touch its reflection.  (I guess the same would happen to a human if it saw a mirror for the first time as an adult.) I did one year of physics at university before switching to maths.  In general I didn't like the practical sessions because they were always at the end of the day, and very long and tiring.  However, on one occasion we got to make our own holograms, and that really did impress me.  IIRC mine was of a 2 pence piece. What I found really interesting, was finding out how they worked.  I don't think we were taught this as such - it was up to us whether we wanted to go off and find out for ourselves.  Anyway,

From: Learn To Speak Mafia About 15 years ago I was working for a small firm making telecoms equipment , and developing from scratch a Voice over IP box.  It was a very simple device to convert SIP internet calls to local analogue POTS lines (Plain Old Telephony Service) and there were just two of us working on the project: Mike the hardware engineer, and me, for the software. The box had a microprocessor running Linux (including a massively hacked version of Linphone for the SIP stack), and it had a DSP to support the codecs (short for Codify/Decodify).  It was quite a fun project (*) . A word about codecs and SIP:  SIP stands for Session Initiation Protocol (**) and is an internet standard allowing two internet peers to start a phone call.  One of the main tasks SIP has to perform is to co-ordinate on which codec to use.  One peer may support GSM, G.729, and G.711, and another may support G.726, GSM, and Speex - in which case the two peers would have to agree to use their on

Curiously, I think the answer is that human males are generally monogamous. Before getting on to that we should ask: what is the excess adipose tissue carried by females of the human species actually for?  There are two naive answers which I've heard expressed in the past: To provide milk for the human infant To attract a mate Neither of these explanations hold water.  Every other mammal that I'm aware of only has swollen glands whilst the offspring are young enough to breastfeed. At all other times the females look more or less similar to the males.  The second explanation leaves open an obvious question too.    Why should a male be attracted to these things in the first place? What does seem to be true, is that - all other things being equal - possession of the aforesaid is an encumbrance, as any well-endowed cave-woman that has ever tried to flee a sabre-toothed tiger might attest. There are cases in nature, however, where encumbrances are carried purely to i

Lockdown reading My lockdown reading list consists of just one book. This might last a long time I thought, so it's my opportunity to make a 2nd stab at understanding Quantum Field Theory. Last time, I bought "Quantum Field Theory for the gifted Amateur" and I learned a lot from it. Mainly that I am not gifted! I got three chapters through it and then gave up on the book, and on quantum field theory. This time round I did my research better and found a much more gentle book: Student Friendly Quantum Field Theory, by Robert D. Klauber . It covers the same material, but takes pains not to lose the reader, by spelling out every ambiguity and subtlety. I'm half way through and feeling quite chuffed with myself. Here I am studying hard, on a sunny day in Lockdown Britain: No, the weights are not mine In this book, and every other in the QFT literature there is a concept of some particles being virtual. What's this about?  Why are some virtual and o

I decided to watch Contagion on the telly the other night.  I thought it might be fun to see how Hollywood's idea of a pandemic matched reality....  Anyway, can you spot the glaring mistake in this clip? That's right!  He said math  when he should have said maths .  Math ith a roman catholic thervith! There was another problem too.... In the exponential phase the numbers infected increases by the same factor each day, rather than squaring each day.  Or to put it another way, the sequence should have been $$ x_n = 2^n $$ and not what he said, which was $$ x_n = 2^{2^{n-1}} $$ Dear Hollywood, I am happy to offer my services as on set math(s) consultant.  I am very cheap.

When it comes to getting action on the climate crisis I think no-one has been more successful than Extinction Rebellion .  I remember at a party one time showing the NASA CO2 graph to a lady who didn't believe it could be real.  "If this were true people would be running around in the streets screaming" she told me.  That's why XR's tactics actually work.  You can hear day in day out about the urgency and severity of the crisis, but while people are carrying on as before it's difficult for the information to break out from the intellectual part of your brain, and occupy the bit that can actually make a difference. I don't have an issue with XR's tactics, but I do worry about how we often talk to the public when we do have their ear. The pie chart above is completely made up, but I think it's about right. A tiny proportion of the general public make up their minds by looking up facts and figures; a slightly larger - but still tiny - number ar

[Or was it the editing...?]  At first glance it appears that this recent news article on the BBC is going to be a complete hatchet job on Professor Jem Bendell, author of the Deep Adaptation paper.  The paper is an honest, if uncomfortable appraisal of the likelihood of civilisational collapse caused by the climate crisis, and a blueprint for how we can work together to survive it as best we can. The first indication it's going to be hatchet job is the title: "The 'climate doomers' preparing for society to fall apart" Clearly, calling someone a "doomer" is a way of dismissing their point of view without actually challenging it.  Of course the BBC have taken the approach of distancing themselves from any responsibility by putting 'climate doomers' in quotes.  That's a standard trick for when you want to say what you think without having to justify it. The first paragraph of the article is in bold , and is highly dismissive of Ben

This reminder has been on a wall in my house for ~15 years As a programmer for 22 years I've fixed thousands of bugs, and created many times more.  Very often it appeared that the problem I was trying to fix had multiple independent causes.  However I have found - almost invariably - that if you dig long enough you'll find a single cause for all the problems you are seeing.  In fact the moment you hit on the right theory is often really obvious because it suddenly explains a whole bunch of other things that have been going wrong!  But, I wondered, can this observation be proven mathematically?  It turns out it can! The Debugger's Theorem If a system that usually works currently isn't working, then it is more likely than not that there's just one thing causing all the observed problems. Proof Let $P_0$ be the probability that the system has no problems, $P_1$ be the probability that one independent problem has occurred, $P_{2+}$ the probability that two

Article in the Telegraph... And now, the punchline...

How fast would you have to fire a cannonball for it to never hit the ground? Newton's very first ideas about gravitational orbits are said to have come about from a thought experiment. A cannonball was known to lose 5 metres of altitude a second after being fired horizontally, but the Earth - being round - curves away from the cannonball as it flies forward. So it occurred to Newton to ask: How fast would the cannonball have to be fired for the curvature to completely compensate for the vertical loss? If a cannonball was fired at this speed it would never lose any altitude, and end up orbiting the Earth. The diagram above shows that the answer can be found using simply trigonometry and comes to $$ \begin{align} v &= \sqrt{gr} \\ &= \sqrt{9.81 ms^{-2} \times 6.371\times 10^6 m} \\ &= 7868\space ms^{-1} \\ &= 17603\space mph \end{align} $$ In general, (non-relativistic) orbits are elliptical The next stage was to look at more general orbit

Theorem of the week: The Hairy Ball Theorem This says you can't comb a hairy ball without introducing discontinuities such as partings or whorls, unless there's a bald spot.  (There's a more mathematical statement below under the heading "theorem".)  The proof is from An Extremely Short Proof of the Hairy Ball Theorem, by P McGrath , but I've put it into my own words, completely removed all maths notation, and added pictures to make it as accessible as possible.  In addition to being extremely short, it's extremely elegant, and somewhat reminiscent of the Ham Sandwich Theorem . Theorem It is not possible to impose a continuous vector field onto a sphere, such that the vectors are all tangential to the surface, unless the field is zero somewhere Proof Let's assume the sphere does have a continuous, tangential, everywhere non-zero vector field, and attempt to derive a contradiction. Draw a small circle around a point p.  Do one lap around

It may not be entirely obvious from the photograph (which I took at night, while hashing ) but this is a wrought iron gate. It opens on to a front garden on Maid's Causeway, Cambridge.  Why?  I don't know.  Has an important physicist lived there?  There's no Blue Plaque , so maybe it's just an enthusiast, like me! What does it mean?  I don't know for certain, but I suspect it is a reference to something similar to the GHSZ variant of the Bell Inequality Test .  The results of this test demonstrate that there are no hidden variables in quantum mechanics.  I say "similar" because, in GHSZ instead of 0 and 1 the spins $\downarrow$ and $\uparrow$ are used, and there's a minus instead of a plus. If you know anything more, please tell me!

Top left box evolves into a superposition of the other two When introduced to quantum physics the first example we encounter is usually that of a single particle.  We are shown that experiment demonstrates a particle left alone evolves into a superposition of states.  These states may be position states or they may be momentum states, or if the particle has spin it may be a superposition of spin states.  It doesn't matter, the point is that fundamental particles can be in a superposition of states.  That's because they are small, we are told, so you wouldn't expect them to behave like big things do, we are told. The next thing we are shown is how the Schroedinger equation governs the evolution of this superposition.  The particle is not usually in every state equally, it is more in one position state (or momentum state, or spin state) than it is in another.  The distribution over these so-called basis states evolves with time and the Schroedinger equa

Is Our Universe Finite? A while ago I drew the pictures above to try to understand current ideas about the size of the universe. The diagrams are based on some pictures I saw in the book " Our Mathematical Universe ". The diagrams show two dimensional slices of four dimensional spacetime. The blue stuff is "inflationary material" which expands at an enormous rate. The current theory of inflation states that universes like ours form as bubbles in the inflationary material as some of the inflationary material changes phase and "evaporates" out as non-inflationary material. An important point is that the sides of this bubble are moving away from each other way too fast for anything - even light - to travel from one side to the other.  The 1st diagram illustrates the point that in this model there is room for more, far more, than one universe. The yellow region in the 2nd and 3rd diagrams is what is known as a light cone. The point in the middle