- Get link
- Other Apps
- Get link
- Other Apps
In 1964 John Stewart Bell proposed an experiment to determine whether
the results of quantum measurements were truly random, or governed by
hidden variables, i.e. state that exists prior to the measurement, but
which we don’t have access to. The experiment involved creating a large
number of EPR pairs, and firing them at two observers, Alice and Bob,
who measure their photon’s polarisation, choosing the $\updownarrow$
direction or the $\nearrow\llap\swarrow$ direction at random.
Determining the result of the experiment involves doing a complex
statistical calculation to see if something called Bell’s inequality is
satisfied or violated. The Bell experiment was first performed by in
1982 by Alain Aspect, and the result, as most commonly interpreted, is
that hidden variables can only exist if Quantum Mechanics is non-local,
i.e. if it supports faster-than-light causality!
Some time after
Bell proposed his experiment, Greenberger, Horne, and Zeilinger
suggested an alternative one to answer the same question. Theirs
involved three entangled particles instead of two, but did away with the
need for any complicated statistics. We shall consider three ways to
look at this experiment. All three approaches lead to the same
predictions, but they provide different insights into what is going on.
Contents
- Version 1: Three spins
- The mathematics
- Version 2: The quantum computer
- The mathematics
- Version 3: Treating Alice, Bob, and Charlie as quantum mechanical systems
- The mathematics
Version 1: Three spins
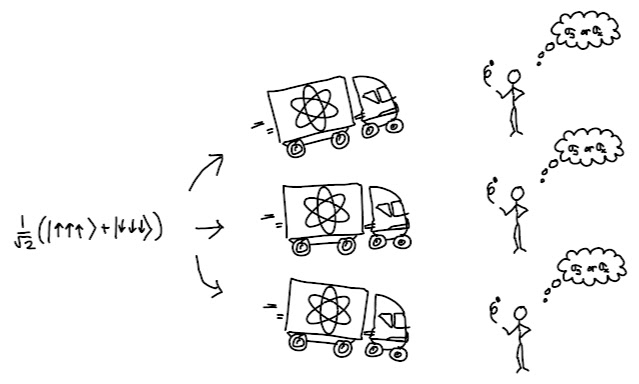
This version is easy to analyse but provides few hints as to why the results are seen, or how to find a way out of the non-locality paradox.
In
this version three spins are entangled in the state $(\lvert
\uparrow\uparrow\uparrow \rangle + \lvert \downarrow\downarrow\downarrow
\rangle)/\sqrt 2$ and are sent, respectively, to Alice, Bob, and
Charlie who are in different locations. After receipt of their spin,
Alice, Bob, and Charlie each toss a coin and measure their spin along
the X-axis if they get tails, and the Y-axis if they get heads.
Critically, all three do this simultaneously so that no information
about the coin toss or the measurement result can reach the others
before they choose an axis or make a measurement.
The results are
that Alice, Bob, and Charlie observe a 50% chance of getting a +1 and a
50% chance of a -1, and this is independent of whether they got H or T
in the coin toss. However, when all three get tails (TTT) multiplying
together the measurements always results in +1, and when just one gets
tails (THH, HTH, or HHT) multiplying them always results in -1. So, for
example (TTT, -1, -1, 1) is possible, but (TTT, -1, -1, -1) is not. This
result seems to either rule out hidden variables or allow for non-local
causality. But why?
Alice knows she gets +1 and -1 each half the
time. As far as she is concerned there are two possibilities: 1) the
result is determined by hidden variables before she makes her
measurement; 2) the result is chosen at random at the exact moment the
measurement is made. She can rule out (1) by a simple thought
experiment. If it were the case then she could label the results she
would get if she were to measure along the X-axis $X_1$, and the result she
would get if she were to measure only the Y-axis as Y1. Likewise Bob
could label his possible results as $X_2$, and $Y_2$, and Charlie could label
his $X_3$, $Y_3$. Alice knows from past experience that $X_1Y_2Y_3$, $Y_1X_2Y_3$ , and
$Y_1Y_2X_3$ are always ‑1. But this would imply that $X_1X_2X_3$ is also always
-1 as it is what you get if you multiply the former 3 terms together.
Since $X_1X_2X_3$ is in fact always +1 Alice can rule out (1). But if her
result is chosen only at the moment she makes the measurement then there
must be some faster-than-light communication to Bob and Charlie. For
example, if they all decide to measure X and Alice measures a -1, then
Bob and Charlie's spins need to get updated instantaneously so that they
cannot both measure the same value, and if she measures +1 then Bob and
Charlie's spins need to get updated instantaneously so that they must
measure the same value.
The mathematics
Let’s see if we can work out why this is the result predicted.
A
short reprise on quantum measurement: A measurement in quantum
mechanics corresponds to a Hermitian operator. These always have a set
of orthonormal eigenvectors, and so any state can be decomposed as a sum
of these. For example, $\sigma_z$ is the operator corresponding to
measurement of a spin along the Z-axis. It's eigenvectors are
$\lvert\uparrow\rangle$ and $\lvert\downarrow\rangle$. If
$\lvert\Psi\rangle$ is a spin pointing along the X-axis then
$\lvert\Psi\rangle = \left(\lvert\uparrow\rangle +
\lvert\downarrow\rangle\right)/\sqrt 2$. According to the Born rule,
eigenvalues are the possible measurement results, and the probability of
each result is given by the square of the magnitude of the
corresponding eigenvector's coefficient. So in this example if we were
to measure $\sigma_z$ when the state is $\lvert\Psi\rangle$ we'd have a
50% chance of getting +1 and a 50% chance of getting -1. A consequence
of this rule is that if the original state is an eigenvector of the
measurement if, and only if, the result is 100% known in advance.
In
the case where we have 3 entangled spins the space is a product space
$V\otimes V\otimes V$, where $V$ is the space for a single spin, and the
measurement that Alice, Bob, and Charlie would make if they got HTH
would be the product operator $\sigma_y\otimes\sigma_x\otimes\sigma_y$.
Now, $\sigma_x$ takes $\lvert\uparrow\rangle$ to
$\lvert\downarrow\rangle$ and vice versa, whereas $\sigma_y$ takes
$\lvert\uparrow\rangle$ to $i\lvert\downarrow\rangle$ and
$\lvert\downarrow\rangle$ to $-i\lvert\uparrow\rangle$. This means that
$\sigma_y\otimes\sigma_x\otimes\sigma_y$ takes
$\left(\lvert\uparrow\uparrow\uparrow\rangle+\lvert\downarrow\downarrow\downarrow\rangle\right)/\sqrt
2$ to
$$
\begin{align*}
&\frac{1}{\sqrt 2}(
\sigma_y\lvert\uparrow\rangle\otimes
\sigma_x\lvert\uparrow\rangle\otimes
\sigma_y\lvert\uparrow\rangle +
\sigma_y\lvert\downarrow\rangle\otimes
\sigma_x\lvert\downarrow\rangle\otimes
\sigma_y\lvert\downarrow\rangle) = \\
&\frac{1}{\sqrt 2}(
i^2
\lvert\downarrow\rangle\otimes
\lvert\downarrow\rangle\otimes
\lvert\downarrow\rangle +
(-i)^2
\lvert\uparrow\rangle\otimes
\lvert\uparrow\rangle\otimes
\lvert\uparrow\rangle) = \\
-&\frac{1}{\sqrt 2}(\lvert\uparrow\uparrow\uparrow\rangle +
\lvert\downarrow\downarrow\downarrow\rangle)
\end{align*}
$$
This
tells us that $(\lvert\uparrow\uparrow\uparrow\rangle +
\lvert\downarrow\downarrow\downarrow\rangle)/\sqrt 2$ is an eigenvector
of $\sigma_y\otimes\sigma_x\otimes\sigma_y$ with eigenvalue -1, i.e.
that when the coins come up HTH, the product of the measurements is 100%
guaranteed to be -1, and likewise for THH, and HHT.
A similar
calculation shows that $(\lvert\uparrow\uparrow\uparrow\rangle +
\lvert\downarrow\downarrow\downarrow\rangle)/\sqrt 2$ is also an
eigenvector of $\sigma_x\otimes\sigma_x\otimes\sigma_x$, but this time
with eigenvalue 1. This tells us that when Alice, Bob, and Charlie
throw TTT the product of their measurements is 100% guaranteed to be +1.
Version 2: The quantum computer
This version is a bit more confusing but more clearly illustrates how destructive interference causes some results to be eliminated from the set of possible outcomes.
In this
version we use a quantum computer. Instead of spins $\lvert \uparrow
\rangle$ and $\lvert \downarrow \rangle$ we talk about qbits $\lvert 0
\rangle$ and $\lvert 1 \rangle$, and instead of products of +1s and -1s
we talk about the parities of 3-tuples such as 011.
In the
diagram above, each horizontal line represents one qbit, and each
rectangle is a "gate". Unlike measurements, which "collapse" the
wavefunction, gates represent a change-over-time of the wavefunction.
Measurement is non-reversible since, for example, a measurement of a
single qbit system leaves it in just one of two states, whereas the
original state space is infinite. By contrast, a gate is completely
reversible, in the same way that the Schrödinger equation is symmetric
in forward and reverse time.
The mathematics
Gates are represented by the following unitary operators:
- The first gate applies to just Alice's qbit and is called a Hadamard gate. It takes
- $\lvert 0\rangle$ to $(\lvert 0\rangle + \lvert 1\rangle)/\sqrt 2$, and
- $\lvert 1\rangle$ to $(\lvert 0\rangle - \lvert 1\rangle)/\sqrt 2$
- The second and third gates are CNOT, or Controlled NOT, operators. These apply to the product space of two qbits. CNOT takes
- $\lvert 0x\rangle$ to $\lvert 0x\rangle$, and
- $\lvert 1x\rangle$ to $\lvert 1\bar{x}\rangle$.
- The $R_x(\pi/2)$ gates rotate a single qbit about the X-axis in the Bloch sphere. The exponents$h_A$, $h_B$, and $h_C$ indicate that Alice, Bob, and Charlie should only implement this gate if they toss heads. This gate takes
- $\lvert 0 \rangle$ to $(\lvert 0\rangle -i \lvert 1\rangle)/\sqrt 2$, and
- $\lvert 1\rangle$ to $(-i\lvert 0\rangle + \lvert 1\rangle)/\sqrt 2$.
- The $R_y(-\pi/2)$ gates rotate a single qbit about the Y-axis in the Bloch sphere. The exponents $t_A$, $t_B$, and $t_C$ indicate that Alice, Bob, and Charlie should only implement this gate if they toss tails. This gate takes
- $\lvert 0 \rangle$ to $(\lvert 0\rangle - \lvert 1\rangle)/\sqrt 2$, and
- $\lvert 1\rangle$ to $(\lvert 0\rangle + \lvert 1\rangle)/\sqrt 2$.
- The final rectangles represent measurement along the Z-axis, which is defined by the eigenvectors $\lvert 0\rangle$ and $\lvert 1\rangle$.
With
this background we can calculate each of the states
$\lvert\Psi_1\rangle$, $\lvert\Psi_2\rangle$, $\lvert\Psi_3\rangle$,
$\lvert\Psi_4\rangle_{hht}$, and $\lvert\Psi_5\rangle_{hht}$ (the hht
subscript indicates that this is the situation in which the coin tosses
obtained the result HHT).
$$
\require{cancel}
\begin{align*}
\lvert \Psi_1 \rangle &= \lvert 000\rangle \\
\\
\lvert \Psi_2 \rangle &= \frac{1}{\sqrt 2}(\lvert 000\rangle +
\lvert 100\rangle) \\
\\
\lvert \Psi_3 \rangle &= \frac{1}{\sqrt 2}(\lvert 000\rangle +
\lvert 111\rangle) \\
\\
\lvert \Psi_4 \rangle_{hht} &= \frac{1}{2\sqrt 2}(\\
&\lvert 000\rangle -i\lvert 010\rangle -i \lvert 100\rangle -
\lvert 110 \rangle \\
-&\lvert 001\rangle -i\lvert 011\rangle -i \lvert 101\rangle +
\lvert 111 \rangle) \\
\\
\lvert \Psi_5 \rangle_{hht}&= \frac{1}{4}(\\
&\cancel{\lvert 000\rangle} -\lvert 001\rangle - i\lvert
010\rangle +i\cancel{\lvert 011 \rangle} \\
-i&\lvert 100\rangle +i\cancel{\lvert 101\rangle} -
\cancel{\lvert 110\rangle} +\lvert 111 \rangle \\
-&\cancel{\lvert 000\rangle} -\lvert 001\rangle -i\lvert
010\rangle -i\cancel{\lvert 011 \rangle} \\
-i&\lvert 100\rangle -i\cancel{\lvert 101\rangle}
+\cancel{\lvert 110\rangle} +\lvert 111 \rangle
)
\end{align*}
$$
This
shows that only parity 1 combinations remain. A similar calculation
for $\lvert \Psi_5 \rangle_{ttt}$ leaves only parity 0 combinations!
This shows how the possible outcomes can be described to be as a result
of interference.
Version 3: Treating Alice, Bob, and Charlie as quantum mechanical systems
Is
there any reason we cannot treat everything in the experiment,
including Alice, Bob, and Charlie, as quantum mechanical? We know the
participants are perfectly isolated from each other by distance and the
speed of light, so there’s really no problem in this. In this treatment
the initial state can be represented as a superposition in which each
term represents a pre-determined outcome. The only problem is that you
have to believe in the multiverse.
The
qbits Alice, Bob, and Charlie start off $\lvert h \rangle$, for heads,
giving an initial state for the entire system of $\lvert \Psi_1 \rangle
=\lvert hhh 000 \rangle$. To get to $\lvert \Psi_2 \rangle$ the lower
subsystem is entangled in the 3-qbit Bell state $(\lvert 000 \rangle +
\lvert 111 \rangle)/\sqrt 2$ as before, but in addition to this each of
Alice, Bob, and Charlie are transformed by Hadamard gates. This leaves
the entire system in the product state
$$
\lvert \Psi_2\rangle = \frac{1}{4}\sum_{a,b,c
\in \{h,t\}}{\lvert abc \rangle} \otimes (\lvert 000 \rangle +
\lvert 111 \rangle)
$$
The
$R_x(\pi/2)$ rotation gates are now controlled gates that only occur if
the corresponding participant state is $\lvert h \rangle$. The $X$ gate
swaps $\lvert h \rangle$ and $\lvert t \rangle$, so the $R_y(-\pi/2)$
are also controlled but only occur if the participant state is $\lvert t
\rangle$. In this version $\lvert \Psi_3 \rangle$ is a complicated
state like
$$
\lvert \Psi_3\rangle = \sum_{a,b,c \in
\{h,t\}}\sum_{x,y,z \in \{0,1\}} \psi_{abcxyz}\lvert abcxyz
\rangle
$$
in
which certain coefficients, such as $\psi_{ttt111}$ or $\psi_{hht110}$
have value 0. This is the multiverse interpretation in which collapse
never occurs!
The mathematics
The
above picture shows no interaction with any classical system and so we
are allowed to treat all the gates as a single unitary operator $U$. If
we were to append a measurement in the computational basis, its operator
would be $Z^{\otimes 6}$ where $Z$ is the pauli Z matrix. We could then
treat the entire circuit as a single measurement. What operator $A$
would that correspond to?
We know that if we were to start off
with state $\lvert \Psi_1 \rangle = U^\dagger \lvert hhh000 \rangle$ the
final result would be 100% guaranteed to be $\lvert hhh000 \rangle$. A
similar thing would be the case for all the other combinations of 3 h’s
and t’s, and 3 0’s and 1’s. The only initial states which have known
final states following a measurement are its eigenvectors. This means we
know the eigenvectors of $A$ must be
$$
U^\dagger \lvert abcxyz \rangle \ \dots a,b,c \in \{h,t\}, x,y,z \in \{0,1\}
$$
Knowing the eigenvectors and eigenvalues uniquely identifies the operator, so we must have that
$$
A = U^\dagger Z ^{\otimes 6} U
$$
In the illustration above we did not start off in an eigenstate of $A$, but instead the state
$$
\lvert \Psi_1 \rangle = \lvert hhh000
\rangle .
$$
If
we were to decompose this using the orthonormal set of eigenvectors
$U^\dagger \lvert abcxyz \rangle $ we would find that all the terms
where there’s one t and two h’s in $abc$, and $xyz$ has parity zero, are
missing. Likewise all the terms where there are three t’s in $abc$, and
$xyz$ has parity one, are missing.
Viewed this way there is no
need to explain the outcomes of any collapse as no collapse occurs.
Subjectively when Alice, Bob, and Charlie come together to compare
results, all that happens is that they determine which term in the
original superposition they were in all along.
- Get link
- Other Apps


Comments
Post a Comment