Maxwell's Daemon

When the 2nd law of thermodynamics was discovered a lot of theorists were understandably suspicious.  It said that entropy always increases with time, or $\frac{dS}{dt} > 0$, but this seems to go against time reversal symmetry, which is a feature of all physical laws. (Okay... in QM you also have to reverse charge and parity in the system too....) 

Amongst those who challenged the new theory was James Clerk Maxwell (he who shed light on light) and he did so with a thought experiment.  Imagine you have a box full of air at a given temperature, and it is divided into two parts.  Between the two is a little door which can be opened and shut by a daemon.  This daemon watches the air molecules speeding towards the door and if the molecule is faster than average and on the LHS he opens the door briefly to let it pass through to the right hand side.  Conversely if the molecule is slower than average and on the RHS the daemon will open the door to let is pass to the left hand side.  Over time the RHS will get hotter and the LHS will get colder.  The total energy of the system will remain the same, but since the system is now more organised the entropy will decrease - contradicting the 2nd law.

A lot of ad-hoc attempts to resolve this problem ensued.  Often the approach was to take a given implementation of the daemon, and then to show how it wouldn't work.  For example collisions between the molecule and the sensor may cause some heat to leak out of the box.  It seemed that any given mechanism could be shown to  fail in its goal of reducing entropy, but it was much harder to show why they all must fail in principle.

To understand why Maxwell's daemon cannot ever reduce entropy it is necessary to treat the daemon himself as part of the system.  Because what the 2nd law says is that "the total entropy of a closed system" will always increase.  If you arbitrarily split a system into two parts (e.g. the daemon and the box of gas) then it is perfectly allowable for the entropy of one part to decrease at the expense of the other.  So, how on earth do you include something as complicated as a miniature daemon when theorizing about changes in entropy?

The first thing we need is a proper definition of entropy.  In classical mechanics a closed system of $N$ distinct particles can be described by listing $3N$ coordinates ($\dagger$), labelled $q_i$, and $3N$ momenta, labelled $p_i$.  In effect the state of the system is described as a point in a $6N$ dimensional phase space.   Sometimes these points are referred to as microstates.  In addition to microstates we can define the macrostate of a system to be a set of parameters that describes the system at the macroscopic scale, such as the temperature and pressure of gas in a box.  One macrostate will comprise of multiple microstates which all look "the same" at the macroscopic scale.  So we can define entropy as the volume of phase space corresponding to the current macrostate, or alternatively the number of microstates in the current macrostate.  A macrostate consisting of more microstates is in a sense more disorganised because there are more ways the individual particles can be given positions and momenta so as to acheive it.

For each point in phase space there is a trajectory passing through it which describes how the system passing through that microstate would evolve in time.  So if you track all the points in a given volume of phase space then the whole volume will evolve into a different shape.  However, Liouville's Theorem states that the total volume will always remain the same.  This is easy to prove from Hamilton's equations of motion ($\dagger^2$)
$$
\begin{align}
\dot{q_i} &= \frac{\partial{H}}{\partial{p_i}} \\
\dot{p_i} &= - \frac{\partial{H}}{\partial{q_i}}
\end{align}
$$

Over a small time $\delta t$ the change in the volume $V = \displaystyle  \prod_{i=1}^N{\Delta q_i \Delta p_i}$ will be
$$
\begin{align}
\delta V &= \displaystyle \sum_{i=1}^N \left( \frac{\delta \Delta q_i}{\Delta q_i}  V + \frac{\delta \Delta p_i}{\Delta p_i}  V \right) \tag{1}
\end{align}$$
But
$$
\begin{align}
\delta \Delta q_i &= \delta t \Delta q_i \frac{\partial \dot{q_i}}{\partial q_i} \\
\implies \delta \Delta q_i &= \delta t \Delta q_i \frac{\partial^2 H}{\partial q_i \partial p_i} \tag{2} \\
\delta \Delta p_i &= \delta t \Delta p_i \frac{\partial \dot{p_i}}{\partial p_i} \\
\implies \delta \Delta p_i &= -\delta t \Delta p_i \frac{\partial^2 H}{\partial p_i \partial q_i} \tag{3} \\
\end{align}$$
And substituting (2) and (3) into (1) gives

$$
\delta V = 0
$$

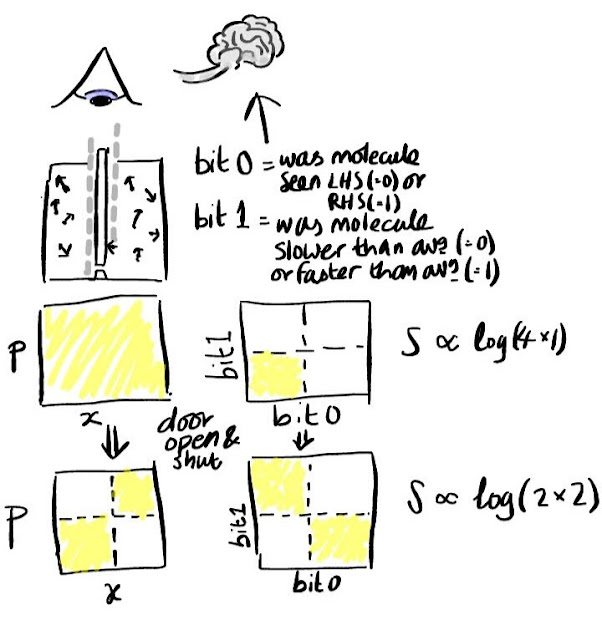
The picture above illustrates this for Maxwell's daemon.  The diagrams on the top show two different slices of phase space prior to the daemon opening the door to let a single molecule pass through.  The slice on the left shows one component of position and one component of momentum for a single gas molecule.  The slice on the right shows the values of two binary digits in the daemon's brain.  The whole of the slice on the left is shaded to indicate that all values are contained within the initial macrostate.  On the right it is only the bottom left quadrant that is coloured indicating that in the initial macrostate the daemon's memory is in its reset configuration (all zeros).

The diagrams on the bottom show the same two slices of phase space, but after the daemon has opened the door briefly to let a molecule pass through.  Since the daemon chose to open the door rather than keep it shut he must have either seen i) a molecule on the LHS moving fast (bits = 01) or ii) a molecule on the RHS moving slow (bits = 10).  In short the volume of phase space occupied by the daemon's brain has doubled.  This perfectly offsets the change in volume in the other slice of phase space which has halved.  Since the two volumes must be multiplied together to get new total volume we find - as Liouville predicted - that the total volume in phase space has not changed.

But what if the daemon resets the binary digits in his brain.  Surely then the volume will fall to half.  Well the task of changing the state of his brain from an initially unknown state to a known one (all zeros) is completely equivalent to the original problem of sorting gas molecules into two groups (high velocity on the RHS and low on the LHS).  So, yes, we could reset the state of his brain, but some other slice of phase space must grow to take up the slack!

So, if the volume of phase space always remains constant, why doesn't the 2nd law read $\frac{dS}{dt} = 0$ rather than $\frac{dS}{dt} > 0$?  Well in that equation the variable $S$ is the volume of phase space corresponding to the current macrostate.  According to Liouville's Theorem if you start off with a nicely defined shape corresponding to an entire macrostate, then no matter how contorted that shape becomes, it's volume remains the same.  So Liouville tells us that if macrostate A evolves into macrostate B - whatever the initial microstate - then macrostate B must occupy at least as much volume in phase space.  And that sounds pretty similar to the 2nd law of thermodynamics.

END

• ($\dagger$)  The coordinates don't have to be spatial degrees of freedom - all that's required is that the $q_i$, and the $\dot{q_i}$ completely define the state of the system.  Likewise, the momenta (which are properly called conjugate momenta) are not in general equal to $m_i\dot{q_i}$.  The general definition is $p_i = \frac{\partial L}{\partial \dot{q_i}}$,  where $L(q_i,\dot{q_i})$ is the lagrangian for the system.  However, it is a common case that the $\dot{q_i}$ only appear in $\frac{1}{2}m_i \dot{q_i}^2$ terms in $L$ and in this case the two definitions match.
• ($\dagger^2$) Where $H(q_i,p_i) = \sum{p_i \dot{q_i}} - L$ is the Hamiltonian, or energy of the system.